Internal Waves 1 - Low frequency
Purpose:
To show the unusual, anisotropic phase and group
velocity properties of internal gravity waves in a density-stratified
fluid.
What Happens:
A tank about 30 cm deep is filled with a salt
stratification of buoyancy period, 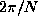 ,
about 6 seconds. A
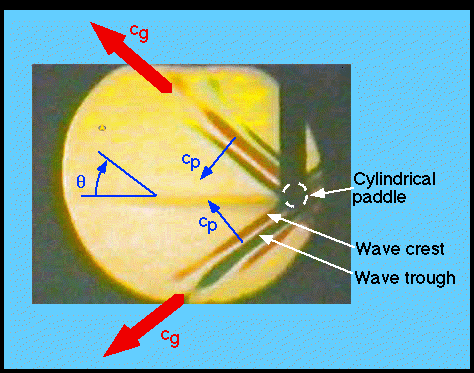
solid cylinder of a few cm diameter runs across the tank at mid depth,
in the right of the field of view (see diagram below). This cylinder
is oscillated horizontally (to the left and right in the diagram) at
frequency less than N, generating internal waves. The flow is
visualized with a schlieren system that shows regions of positive
isopycnal slope in red, and negative isopycnal slope in green. Slopes
close to zero show as yellow. The movie is in time lapse, so that the
waves appear to have higher than real frequency. The movie starts
from rest, and after the paddle motion begins, the wave field starts
to fill the tank outwards from the paddle. In the movie clip, wave
energy appears to travel at an angle
,
about 6 seconds. A
solid cylinder of a few cm diameter runs across the tank at mid depth,
in the right of the field of view (see diagram below). This cylinder
is oscillated horizontally (to the left and right in the diagram) at
frequency less than N, generating internal waves. The flow is
visualized with a schlieren system that shows regions of positive
isopycnal slope in red, and negative isopycnal slope in green. Slopes
close to zero show as yellow. The movie is in time lapse, so that the
waves appear to have higher than real frequency. The movie starts
from rest, and after the paddle motion begins, the wave field starts
to fill the tank outwards from the paddle. In the movie clip, wave
energy appears to travel at an angle  from the horizontal, and
the wave crests sweep at right angles to this direction.
from the horizontal, and
the wave crests sweep at right angles to this direction.
Physics of the phenomenon:
a. Dispersion relationship
In a density-stratified fluid at
rest, each fluid parcel sits at the level of others of the same
density. Lighter parcels sit at a higher level, and denser ones lie
below. When the parcel is displaced upwards, it is heavier (more
dense) than the surrounding fluid, and the slightly larger
gravitational force on that fluid parcel pulls it back down. This is
just the same as the settling of a blob of vinegar in a shaken bottle
of oil/vinegar salad dressing. The fluid parcel's inertia causes it
to overshoot it's starting position, so that when it lies below the
rest level, it is lighter (less dense) than its surroundings. The
parcel now floats upwards towards its rest level. The fluid parcel
therefore bobs up and down, pushed by the buoyancy force generated by
gravity acting on slight density differences, and balanced by the
inertial forces due to the fluid's mass. The frequency of this
oscillation is called the buoyancy frequency, N:
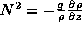
where g is the acceleration of the Earth's gravity field,
9.8 ms-2,
and  is the density of the fluid at rest.
is the density of the fluid at rest.
The buoyancy
oscillation described above is a special case of an internal gravity
wave. If one considers disturbances of the form
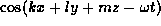 ,
then those disturbances must obey the dispersion relation for internal
gravity waves (Phillips, 1966):
,
then those disturbances must obey the dispersion relation for internal
gravity waves (Phillips, 1966):
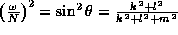
This means that the frequency depends on the angle  , which is
the angle the wave crests and the wave energy flux or group velocity
make to the horizontal. Waves of a specific frequency can only
propagate at a specific angle. Note also that since
, which is
the angle the wave crests and the wave energy flux or group velocity
make to the horizontal. Waves of a specific frequency can only
propagate at a specific angle. Note also that since 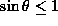 , the maximum allowed frequency is N, the frequency of the
buoyancy oscillation.
, the maximum allowed frequency is N, the frequency of the
buoyancy oscillation.
b. Group velocity:
The energy is carried outwards from the paddle by the group velocity,
which is restricted to the characteristic angles 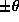 ,
determined by the dispersion relation with
,
determined by the dispersion relation with  paddle frequency. The
wave disturbance builds out from the paddle, but only becomes
significant in "ray" regions at the characteristic angle
paddle frequency. The
wave disturbance builds out from the paddle, but only becomes
significant in "ray" regions at the characteristic angle  from
the paddle. Regions between the rays have very little wave energy.
from
the paddle. Regions between the rays have very little wave energy.
c. Phase velocity
The wave "crests", or lines of constant phase, are the red and green
bands. Note that they sweep perpendicular to the energy rays: the
phase velocity is perpendicular to the group velocity. Note also the
sign: waves above the paddle, with upward moving energy flux, have
downward phase propagation, and vice versa. although the phase
velocity is the most visible part of the wave propagation, we can
never forget that the energy goes with the group velocity, not the
phase.
References:
Phillips, O.M. 1966. The dynamics of the upper ocean. Cambridge
University Press.
Lighthill, James, 1978. (Chapters 3 and 4.) Waves in fluids. Cambridge
University Press.
Credits:
Movie and text - Barry Ruddick
Digitization of movie - Dave Hebert
Load and run low frequency internal waves movie
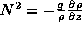
![]() is the density of the fluid at rest.
is the density of the fluid at rest.![]() ,
then those disturbances must obey the dispersion relation for internal
gravity waves (Phillips, 1966):
,
then those disturbances must obey the dispersion relation for internal
gravity waves (Phillips, 1966):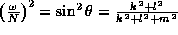
![]() , which is
the angle the wave crests and the wave energy flux or group velocity
make to the horizontal. Waves of a specific frequency can only
propagate at a specific angle. Note also that since
, which is
the angle the wave crests and the wave energy flux or group velocity
make to the horizontal. Waves of a specific frequency can only
propagate at a specific angle. Note also that since ![]() , the maximum allowed frequency is N, the frequency of the
buoyancy oscillation.
, the maximum allowed frequency is N, the frequency of the
buoyancy oscillation.